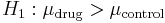Null hypothesis

The practice of science involves formulating and testing hypotheses, assertions that are falsifiable using a test of observed data. The null hypothesis typically proposes a general or default position, such as that there is no relationship between two measured phenomena,^[1] or that a potential treatment has no effect.^[2] The term was originally coined by English geneticist and statistician Ronald Fisher.^[3] It is typically paired with a second hypothesis, the alternative hypothesis, which asserts a particular relationship between the phenomena. Jerzy Neyman and Egon Pearson formalized the notion of the alternative. The alternative need not be the logical negation of the null hypothesis and is the predicted hypothesis you would get from the experiment. The use of alternative hypotheses was not part of Fisher's formulation, but became standard.

Hypothesis testing works by collecting data and measuring how probable the data is, assuming the null hypothesis is true. If the data is very improbable (usually defined as observed less than 5% of the time), then the experimenter concludes that the null hypothesis is false. If the data do not contradict the null hypothesis, then no conclusion is made. In this case, the null hypothesis could be true or false; the data gives insufficient evidence to make any conclusion.

For instance, a certain drug may reduce the chance of having a heart attack. Possible null hypotheses are "this drug does not reduce the chances of having a heart attack" and "this drug has no effect on the chances of having a heart attack". The test of the hypothesis consists of administering the drug to half of the people in a study group as a controlled experiment. If the data show a statistically significant change in the people receiving the drug, the null hypothesis is rejected.

The choice of null hypothesis is critical. Consider the question of whether a tossed coin is fair (i.e. that on average it lands heads up 50% of the time). A potential null hypothesis is "this coin is not biased towards heads". The experiment is to repeatedly toss the coin. A possible result of 5 tosses is 5 heads. Under this null hypothesis, the data are considered unlikely (with a fair coin, the probability of this is 3%). The data refutes the null hypothesis: the coin is biased.

Alternatively, the null hypothesis, "this coin is fair" allows runs of tails as well as heads, increasing the probability of 5 of a kind to 6%, which is no longer statistically significant, preserving the null hypothesis.^[4]

This example illustrates one hazard of hypothesis testing: evaluating a large number of true null hypotheses against a single dataset is likely to spuriously reject some of them because of the inevitable noise in the data. However, formulating the null hypothesis before collecting data, rejects a true null hypothesis only a small percent of the time.

Testing for differences

In scientific and medical research, null hypotheses play a major role in testing the significance of differences in treatment and control groups. This use, while widespread, offers several grounds for criticism, including straw man, Bayesian criticism and publication bias.

The typical null hypothesis at the outset of the experiment is that no difference exists between the control and experimental groups (for the variable being compared). Other possibilities include:

• that values in samples from a given population can be modeled using a certain family of statistical distributions.
• that the variability of data in different groups is the same, although they may be centered around different values.

Example

Given the test scores of two random samples of men and women, does one group differ from the other? A possible null hypothesis is that the mean male score is the same as the mean female score:

where:

= the null hypothesis

= the mean of population 1, and

= the mean of population 2.

A stronger null hypothesis is that the two samples are drawn from the same population, such that the variance and shape of the distributions are also equal.

Directionality

Quite often statements of null hypotheses appear not to have a "directionality", namely, that values are identical. However, null hypotheses can and do have "direction"—in many instances statistical theory allows the formulation of the test procedure to be simplified, thus the test is equivalent to testing for an exact identity. For instance, when formulating a one-tailed alternative hypothesis, application of Drug A will lead to increased growth in patients, then the true null hypothesis is the opposite of the alternative hypothesis i.e. application of Drug A will not lead to increased growth in patients. The effective null hypothesis will be application of Drug A will have no effect on growth in patients.

In order to understand why the effective null hypothesis is valid, it is instructive to consider the above hypotheses. The alternative predicts that exposed patients exposed experience increased growth compared to the control group. That is,

where:

= the patients' mean growth.

The effective null hypothesis is .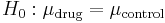

The true null hypothesis is .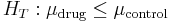

The reduction occurs because, in order to gauge support for the alternative, classical hypothesis testing requires calculating how often the results would be as or more extreme than the observations. This requires measuring the probability of rejecting the null hypothesis for each possibility it includes and second to ensure that these probabilities are all less than or equal to the test's quoted significance level. For reasonable test procedures the largest such probability occurs on the region boundary 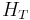, specifically for the cases included in only. Thus the test procedure can be defined (that is the critical values can be defined) for testing the null hypothesis 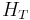exactly as if the null hypothesis of interest was the reduced version .

Fisher said, "the null hypothesis must be exact, that is free of vagueness and ambiguity, because it must supply the basis of the 'problem of distribution,' of which the test of significance is the solution", implying a more restrictive domain for .^[5] According to this view, the null hypothesis must be numerically exact—it must state that a particular quantity or difference is equal to a particular number. In classical science, it is most typically the statement that there is no effect of a particular treatment; in observations, it is typically that there is no difference between the value of a particular measured variable and that of a prediction. The majority of null hypotheses in practice do not meet this "exactness"criterion. For example, consider the usual test that two means are equal where the true values of the variances are unknown—exact values of the variances are not specified.

Most statisticians believe that it is valid to state direction as a part of null hypothesis, or as part of a null hypothesis/alternative hypothesis pair.^[6] The logic is quite simple: if the direction is omitted, then if the null hypothesis is not rejected it is quite confusing to interpret the conclusion. For example, consider an that claims the population mean = 10, with the one-tailed alternative mean > 10. If the sample evidence obtained through x-bar equals −200 and the corresponding t-test statistic equals −50, what is the conclusion? Not enough evidence to reject the null hypothesis? Surely not! But we cannot accept the one-sided alternative in this case. Therefore, to overcome this ambiguity, it is better to include the direction of the effect if the test is one-sided. The statistical theory required to deal with the simple cases dealt with here, and more complicated ones, makes use of the concept of an unbiased test.

Sample size

Statistical hypothesis testing involves performing the same experiment on multiple subjects. The number of subjects is known as the sample size. The procedure depends on the size. Even if a null hypothesis does not hold for the population, an insufficient sample size may prevent its rejection. Minimum sample size depends on the statistical power of the test, the effect size that the test must reveal and the desired significance level. The significance level is the probability of rejecting the null hypothesis when the null hypothesis holds in the population. The statistical power is the probability of rejecting the null hypothesis when it does not hold in the population (i.e., for a particular effect size).

See also

• Counternull
• Statistical hypothesis testing

References

Further reading

• Adèr, H. J.; Mellenbergh, G. J. & Hand, D. J. (2007). Advising on research methods: A consultant’s companion. Huizen, The Netherlands: Johannes van Kessel Publishing. ISBN 9079418013 .

External links

• HyperStat Online: Null hypothesis